Equazioni di secondo grado pure – Esercizio 2
Equazioni di secondo grado pure
Risolvere la seguente equazione di secondo grado:
L’equazione è di secondo grado e inoltre è pura perchè manca il termine col coefficiente x. Per risolvere questo tipo di equazioni ricordiamo che lo scopo e quello di “isolare” l’incognita x (applicando i principi delle equazioni) in modo che rimanga sola al primo membro. Iniziamo quindi a spostare il 45 al secondo membro:
Come secondo passaggio, notiamo che moltiplicato alla x c’è il numero 5. Per toglierlo possiamo moltiplicare primo e secondo membro per 1/5 senza cambiare il risultato:
Infine togliamo il quadrato per trovare le soluzioni mettendo sotto radice primo e secondo membro.
Esercizio 2
Risolvere:
![]()
Applicando il secondo principio di equivalenza possiamo scrivere:
![]()
quindi
![]()
![]()
![]()
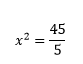

Verissimo, ha ragione Lory!!! Risultato: + – 3/7