Esercizio dominio secondo grado 3
Esercizio dominio secondo grado. Trova il dominio della seguente funzione tenendo presente che dovrai risolvere solo equazioni o disequazioni di secondo grado.
![]()
Per trovare il dominio della funzione, ovvero l’insieme dei valori che hanno un’associazione con altri valori nel codominio, dobbiamo classificare questa funzione. Poichè sono presenti una frazione e una radice quadrata che coinvologono la variabile x la funzione è sia fratta che irrazionale. Le condizioni da imporre sono in questo caso due:
![]()
perchè il contenuto di una radice con un indice pari non può essere negativo e anche
![]()
perchè il denominatore di una frazione non può essere uguale a zero.
Dato che le condizioni devono essere soddisfatte entrambe le inseriamo in un sistema:
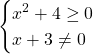
Risolviamo la prima disequazione:
![]()
Poichè è una disequazione di secondo grado calcoliamo il ![]() e risolviamo l’equazione associata.
e risolviamo l’equazione associata.
![]()
![]()
Il ![]() è negativo e il termine
è negativo e il termine ![]() dell’espressione è positivo come il verso della disequazione
dell’espressione è positivo come il verso della disequazione ![]() (sono concordi). Per questo possiamo concludere che questa espressione è sempre positiva. Ciò si può facilmente notare perchè un termine al quadrato (sempre positivo) sommato ad un termine poitivo (4) non potrà mai essere negativo. La soluzione è quindi:
(sono concordi). Per questo possiamo concludere che questa espressione è sempre positiva. Ciò si può facilmente notare perchè un termine al quadrato (sempre positivo) sommato ad un termine poitivo (4) non potrà mai essere negativo. La soluzione è quindi:
![]()
La seconda è una equazione di primo grado
![]()
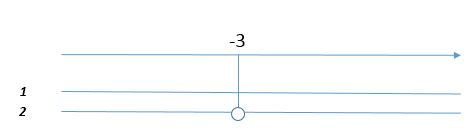
Mettiamo ora insieme le due soluzioni nel sistema e consideriamo l’intersezione di tutte le soluzioni:
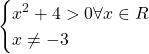
![]()
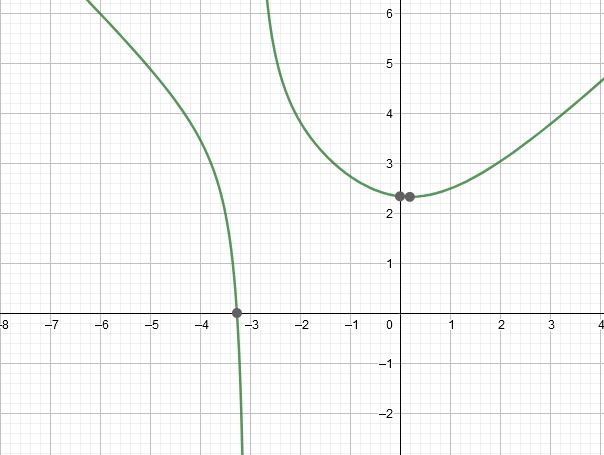
Dal grafico della funzione abbiamo una conferma di quanto studiato precedentemente notando che il valore -3 è escluso dal dominio della funzione.
Torna a dominio funzioni secondo grado
Prova a calcolare la funzione anche tu su GeoGebra!