Equazioni irrazionali Esercizio 4

19 Giugno 2019 gpalmieri Equazioni irrazionali

Quarto esercizio sulle equazioni irrazionali esercizio. Risolvi la seguente equazione irrazionale:

$\sqrt{4-x^2}=x+1$

Questa equazione è del secondo tipo perchè al secondo membro è presente un polinomio con un incontrita in x. Per risolvere l’intera disequazione bisogna quindi risolvere il sistema:

$\begin{cases}B\geq0\\A=B^2\end{cases}$

$\begin{cases}x+1\geq0\\4-x^2=(x+1)^2\end{cases}$

$\begin{cases}x\geq-1\\4-x^2=x^2+2x+1\end{cases}$

$\begin{cases}x\geq-1\\-x^2-x^2-2x+4-1=0\end{cases}$

$\begin{cases}x\geq-1\\-2x^2-2x+3=0\end{cases}$

$\begin{cases}x\geq-1\\2x^2+2x-3=0\end{cases}$

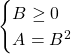
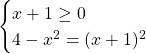
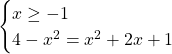
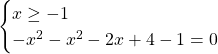
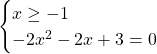
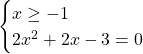
Concentriamoci ora sulla risoluzione della seconda equazione:

$2x^2+2x-3=0$

$\Delta = b^2 - 4 a c$

$\Delta = 4 - 4(2)(-3)$

$\Delta = 4 + 24 = 28$

Poichè il delta è positivo possiamo affermare che questa equazione ha due soluzioni reali e distinte. Le possiamo calcolare nel seguente modo:

$x1,2= \frac{-2 \pm \sqrt{28}}{4}$

$\begin{cases}x\geq-1\\x1,2= \frac{-2 \pm \sqrt{28}}{4}\end{cases}$

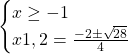
Poichè possiamo accettare solo soluzioni maggiori di -1 l’unica soluzione ammissibille è:

$x =\frac{-2 + \sqrt{28}}{4}$

Ritorna a equazioni irrazionali

Comments

comments

Lascia un commento equazioni irrazionali

L	M	M	G	V	S	D
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

Equazioni irrazionali Esercizio 4

Comments

Lascia un commento Annulla risposta