Studio del segno di una funzione – Esercizio 9
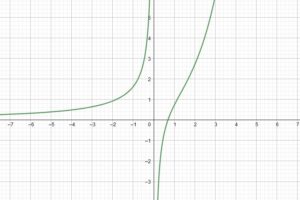
Studio del segno. Studiare il segno della seguente funzione:
Questa funzione è una funzione esponenziale e fratta in quanto la variabile indipendente (x) si trova al denominatore della funzione e anche come argomento di una potenza.
Dominio
Il dominio della funzione si calcola escludendo tutti quai valori che annullano il denominatore:
In definitiva il dominio è:
Segno
Studiare il segno vuol dire vedere quando la funzione è positiva e quando invece è negativa. Significa quindi risolvere la seguente disequazione:
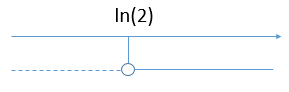
Studio Numeratore
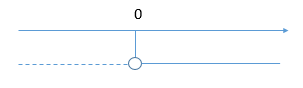
Studio Denominatore
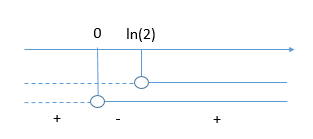
Risultato Finale:
La funzione è quindi positiva per tutti i valori di x tali che o
mentre è negativa per tutti i valori di x tali che
.
Torna a segno di una funzione