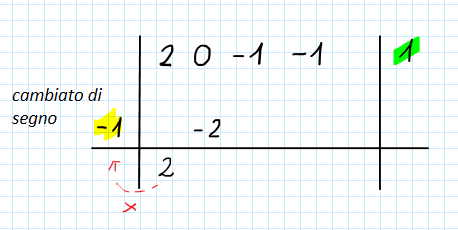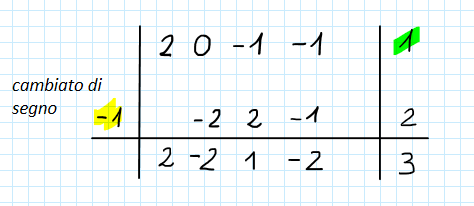Divisione con metodo di Ruffini
Esegui la seguente divisione col metodo di Ruffini:
Per prima cosa controlliamo che i polinomi siano ordinati e completi. In questo caso poichè manca il termine con la base 
e l’esponente 
lo aggiungiamo:
Sistemiamo ora i coefficienti nella tabella per poi iniziare a svolgere i calcoli:
Abbassiamo il primo termine e moltiplichiamo per il 
:
Effettuiamo la somma e proseguiamo con l’altra moltiplicazione:
Infine:
Utilizziamo i coefficienti rimasti in tabella per i termini del polinomio quoziente. L’esponente del primo termine sarà quello del polinomio dividendo originale (
) abbassato di una unità (quindi diventerà ):
Quoziente: 
Resto:
Clicca qui per la teoria.
Torna a divisione polinomi esercizi