Disequazioni di secondo grado fratte – Esercizi
Disequazioni di secondo grado fratte – Esercizi
Le disequazioni di secondo grado fratte si presentano nella forma:
![]() oppure
oppure ![]()
dove N(x) e D(x) sono due polinomi di cui almeno uno è di secondo grado.
Per risolvere questo tipo di disequazioni è necessario portare la disequazione in una delle forme viste precedentemente e studiare separatamente il segno del numeratore e del denominatore. Al termine dello studio bisogna effettuare il prodotto dei segni e individuare gli intervalli di soluzione. Vediamo un esempio per comprendere meglio il processo di risoluzione delle disequazioni di secondo grado fratte:
Esempio
Risolvere la seguente disequazione:
![]()
Come prima cosa notiamo che la disequazione non è in forma normale. Procediamo compiendo i passi necessari per portarla e studiarla.
1. Scomposizione dei denominatori
Tutti i denominatori vanno scomposti per calcolare correttamente il mcm fra essi. Nel nostro caso il primo denominatore (![]() ) non può essere ulteriormente scomposto mentre il secondo è scomponibile:
) non può essere ulteriormente scomposto mentre il secondo è scomponibile:
![]() (regola della differenza di due quadrati)
(regola della differenza di due quadrati)
Dopo aver scomposto i denominatori la disequazione sarà la seguente:
![]()
2. Calcolo del mcm fra i vari denominatori
Possiamo ora individuare il minimo comune multiplo fra i denominatori. I vari fattori sono: ![]() . Secondo la regola dobbiamo predendere tutti i fattori una sola volta con l’esponente maggiore. Quindi la disequazione divente la seguente:
. Secondo la regola dobbiamo predendere tutti i fattori una sola volta con l’esponente maggiore. Quindi la disequazione divente la seguente:
![]()
3. Semplificazione numeratore e denominatore
![]()
![]()
![]()
4. Studio del segno di numeratore e denominatore
Per studiare il segno conviene sempre studiare sempre la diguaglianza ![]() e
e ![]() ovverso è utile vedere quando il numeratore e il denominatore sono positivi
ovverso è utile vedere quando il numeratore e il denominatore sono positivi
Numeratore:
![]()
Per risolvere la disequazione trovo il delta:
![]()
![]()
Il valore del delta è positivo quindi posso individuare le due radici dell’equazione associata che sono
![]()
![]()
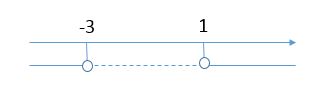
Poichè il termine ![]() della disequazione è positivo (pari ad 1) e il verso della disequazione è maggiore si prendono le soluzioni esterne:
della disequazione è positivo (pari ad 1) e il verso della disequazione è maggiore si prendono le soluzioni esterne:
Denominatore:
Al denominatore sono presenti due fattori costituiti da due binomi e posso studiare per facilità il segno separatamente:
![]()
![]()
e
![]()
![]()
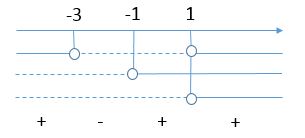
In definitiva facendo il prodotto dei segni generale ottengo:
e poichè il segno della disequazione originaria e maggiore considero come soluzione
![]() v
v ![]() v
v ![]()
Esercizi
Torna a disequazioni di secondo grado