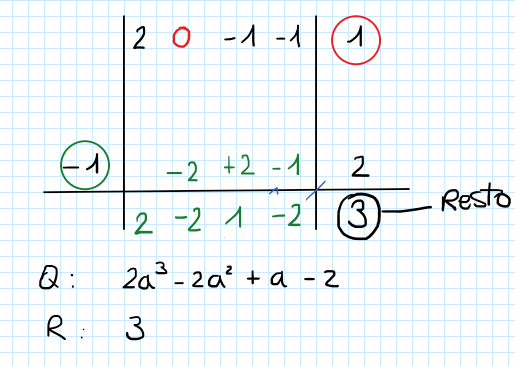Divisione polinomi esercizi
Divisione polinomi esercizi
In questa sezione sono presenti degli esercizi svolti sulle divisioni fra polinomi. Un polinomio può essere diviso per un monomio, oppure per un altro polinomio o infine per un binomio del tipo ![]() con
con ![]() numero reale e quindi l’operazione può essere svolta col metodo di Ruffini. Se non hai molto chiaro l’argomento visita l’area dedicata alla teoria (divisione polinomi esercizi)
numero reale e quindi l’operazione può essere svolta col metodo di Ruffini. Se non hai molto chiaro l’argomento visita l’area dedicata alla teoria (divisione polinomi esercizi)
Divisione polinomio per monomio
Per dividere un polinomio per un monomio è necessario dividere ogni singolo termine del polinomio per il monomio.
![]()
![]()
![]()
| Numero | Esercizio | |
|---|---|---|
| 1 | Vai | |
| 2 | Vai | |
| 3 | Vai | |
| 4 | Vai | |
| 5 | Vai | |
| 6 | Vai |
Divisione polinomio per polinomio
Per dividere due polinomi è necessario utilizzare una tabella per l’operazione.
![]()
| Numero | Esercizio | |
|---|---|---|
| 1 | Vai | |
| 2 | Vai | |
| 3 | Vai | |
| 4 | Vai | |
| 5 | Vai | |
| 6 | Vai |
Divisione con metodo di Ruffini
Le divisioni di un polinomio per un binomio del tipo ![]() con
con ![]() numero reale qualsiasi, si possono risolvere col metodo di Ruffini.
numero reale qualsiasi, si possono risolvere col metodo di Ruffini.
![]()
| Numero | Esercizio | |
|---|---|---|
| 1 | Vai | |
| 2 | Vai | |
| 3 | Vai | |
| 4 | Vai | |
| 5 | Vai | |
| 6 | Vai |
Torna a polinomi