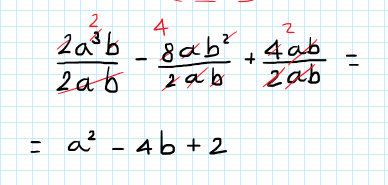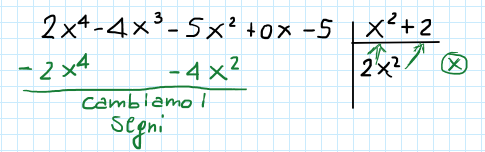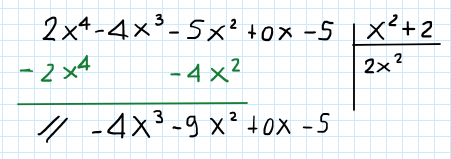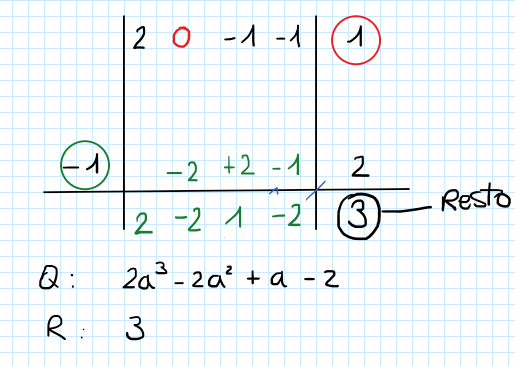Divisione polinomi
Un polinomio A si dice divisibile per un polinomio ![]() (non nullo), se esiste un polinomio
(non nullo), se esiste un polinomio ![]() che, moltiplicato per
che, moltiplicato per ![]() , dà come risultato
, dà come risultato ![]() :
:
![]()
![]() si dice quoziente della divisione
si dice quoziente della divisione ![]()
Facciamo un esempio per meglio comprendere questa regola. Supponiamo di avere i seguenti polinomi:
![]()
![]()
Il risultato della divisione ![]() è
è ![]() perchè:
perchè:
![]() ovvero
ovvero ![]()
![]()
Affinchè un polinomio possa essere divisibile per un altro polinomio è necessario che sia di grado uguale o maggiore. Il polinomio ![]() non sarà quindi certamente divisibile per il polinomio
non sarà quindi certamente divisibile per il polinomio ![]() .
.
Divisione fra polinomio e monomio
Un caso particolare di divisione è quella fra polinomi e monomi. Vediamo un esempio
![]()
Per effettuare questa divisione è necessario dividere ogni termine del polinomio per il monomio:
![]()
Il risultato finale sarà quindi:
![]()
Divisione fra due polinomi
Dati due polinomi A e B esistono sempre due polinomi Q e R (e sono unici) tali che
![]()
Per dividere i polinomi è necessario che abbiano la stessa variabile letterale. Consideriamo la seguente divisione:
![]()
Passo 1
Ordinare tutte le lettere con grado decrescente:
Il polinomio risulterà essere:
![]()
Controllare la completezza del polinomio. In questo caso manca il termine di x con esponente pari ad 1:
Il polinomio da dividere sarà quindi:
![]()
Passo 2
Per prima cosa dividiamo il termine di grado maggiore del dividendo per quello di grado maggiore del divisore:
Passo 3
In seguito moltiplichiamo il risultato per il divisore e cambiamo i segni:
Passo 4
Procediamo ora nello stesso modo reiterando i passaggi:
Regola di Ruffini
E’ possibile semplificare l’algoritmo della divisione nel caso in cui il divisore sia del tipo ![]() dove
dove ![]() rappresenta un numero reale qualsiasi. Vediamo passo per passo come dividere due polinomi con la regola di Ruffini:
rappresenta un numero reale qualsiasi. Vediamo passo per passo come dividere due polinomi con la regola di Ruffini:
![]()
Disponiamo tutti i coefficienti del polinomio dividendo completando con 0 laddove mancano i termini di un certo grado. Nell’esercizio manca il coefficiente numerico di grado 3 e quindi consideriamo il termine ![]() .
.
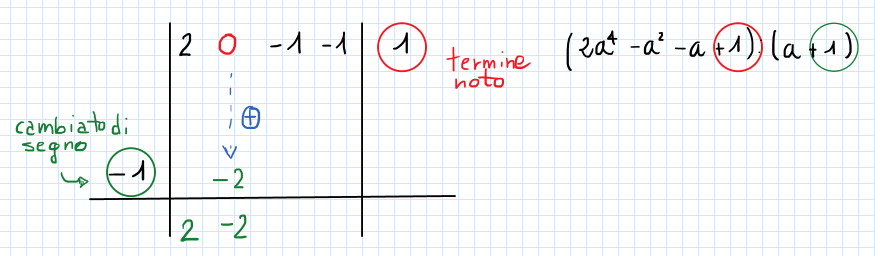
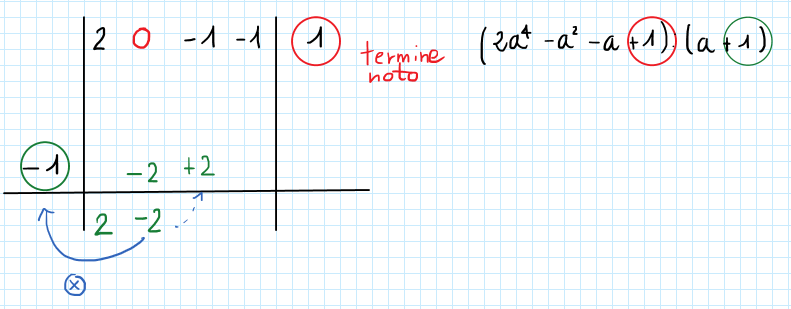
Passo 1
Abbassiamo il primo termine copiandolo al fondo della tabella:
Passo 2
Effettuiamo la moltiplicazione del numero per il coefficiente ![]() e riportiamo il risultato in tabella come indicato:
e riportiamo il risultato in tabella come indicato:
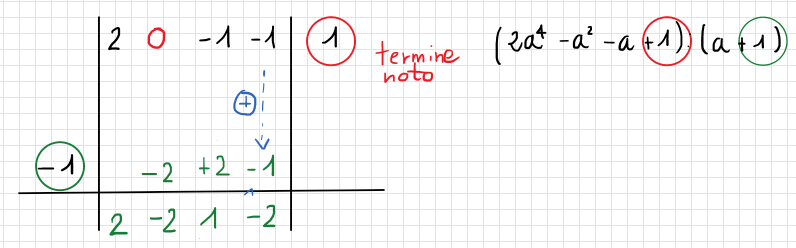
Passo 3
Effettuiamo l’operazione di addizione fra i termini in corrispondenza:
Passo 4
Proseguiamo nello stesso modo reiterando i passaggi:
Passo finale
Al termine delle operazioni l’ultimo numero che rimane in tabella è il resto della divisione. Per ottenere invece il quoziente utilizziamo i coefficienti in tabella e associamo la parte letterale partendo dal grado del polinomio originale meno uno. In questo caso poichè il grado era 4 partiamo dal grado 3.
Il risultato sarà quindi:
![]()
e il resto ![]()
Torna a polinomi