Operazioni matrici

Operazioni matrici

Dati n*m numeri, la tabella che li ordina in m righe ed n colonne viene detta matrice. Ogni numero nella matrice viene detto elemento della matrice ed occupa una posizione identificata dal numero di riga e dal numero di colonna.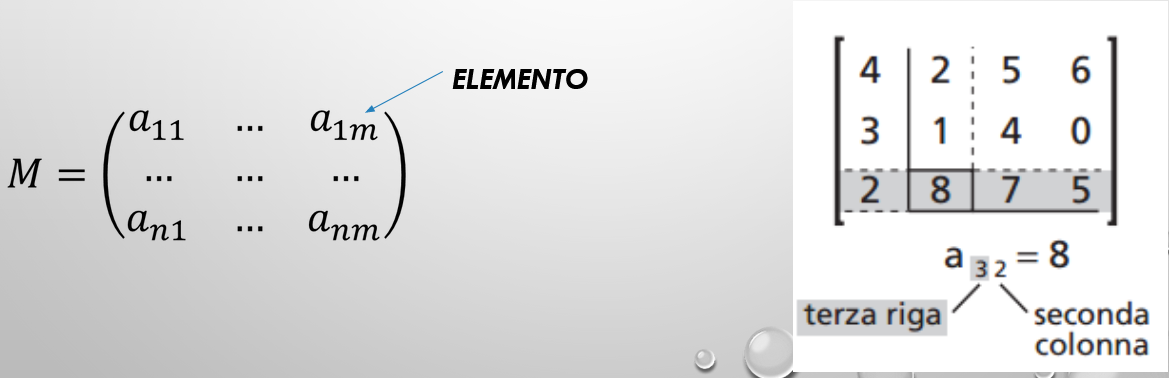

Fra due o più matrici è possibile effettuare delle operazioni.

Addizione

La prima operazione che analizziamo è l’addizione. La somma di due matrici A e B dello stesso tipo è una terza matrice C=A+B dello stesso tipo i cui elementi sono la somma degli elementi corrispondenti delle due matrici.

\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix} + \begin{bmatrix}a^{'}&b^{'}&c^{'}\\d^{'}&e^{'}&f^{'}\end{bmatrix} = \begin{bmatrix}a+a^{'}&b+b^{'}&c+c^{'}\\d+d^{'}&e+e^{'}&f+f^{'}\end{bmatrix}

Ad esempio:

\begin{bmatrix}1&-3&4\\2&-7&1\end{bmatrix} + \begin{bmatrix}-2&-1&7\\4&-5&10\end{bmatrix} = \begin{bmatrix}1-2&-3-1&4+7\\2+4&-7-5&1+10\end{bmatrix} =

=\begin{bmatrix}-1&-4&11\\6&-12&11\end{bmatrix}

Dobbiamo ricordare che l’addizione fra matrici si può effettuare solo se sono dello stesso tipo, altrimenti non è possibile farla.

Sottrazione

La differenza di due matrici si può definire come la somma della prima matrice con l’opposta della seconda:

A=\begin{bmatrix}1&4\\-2&3\\6&-5\end{bmatrix}

B=\begin{bmatrix}-1&3\\4&2\\-5&1\end{bmatrix}

A-B=A+(-B) = \begin{bmatrix}2&1\\-6&1\\11&-6\end{bmatrix}

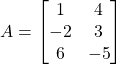
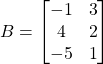
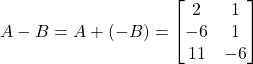
Moltiplicazione

Moltiplicazione per un numero k

Il prodotto di una matrice per un numero reale k è una matrice dello stesso tipo i cui elementi sono tutti moltiplicati per k.

k\cdot\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix} = \begin{bmatrix}k\cdot a&k\cdot b&k\cdot c\\k\cdot d&k\cdot e&k\cdot f\end{bmatrix}

Ad esempio:

3\cdot\begin{bmatrix}2&-1&0\\-5&4&-3\end{bmatrix} = \begin{bmatrix}6&-3&0\\-15&12&-9\end{bmatrix}

Moltiplicazione Riga per Colonna

\begin{bmatrix}a&b&c\end{bmatrix}\cdot\begin{bmatrix}d\\e\\f\end{bmatrix} = \begin{bmatrix}a\cdot d+b\cdot e+c\cdot f\end{bmatrix}

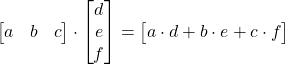
Ad esempio:

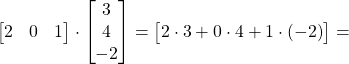\begin{bmatrix}2&0&1\end{bmatrix}\cdot\begin{bmatrix}3\\4\\-2\end{bmatrix} = \begin{bmatrix}2\cdot 3+0\cdot 4+1\cdot (-2)\end{bmatrix} =\begin{bmatrix}4 \end{bmatrix}<h4>Moltiplicazione fra due matrici</h4> Il prodotto di una matrice A di tipo m x n per una matrice B di tipo n x p è una matrice C di tipo m x p, il cui elementoc_{h,k}è dato dal prodotto della riga numero h della prima matrice per la colonna numero k della seconda matrice. <a href="http://www.eserciziario.eu/wp-content/uploads/2019/11/Cattura-1.jpg"><img class="alignnone size-full wp-image-8626" src="http://www.eserciziario.eu/wp-content/uploads/2019/11/Cattura-1.jpg" alt="" width="609" height="175" /></a> Ad esempio:\begin{bmatrix}2&0&1\\-1&-2&3\end{bmatrix}\cdot\begin{bmatrix}1&0&3&0\\5&-1&4&2\\0&1&-2&3\end{bmatrix}  = \begin{bmatrix}a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4}\\a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4}\end{bmatrix}La matrice prodotto avrà 2 righe perchè è il numero di righe della prima matrice e 4 colonne perchè è il numero di colonne della seconda matrice. Ogni elemento potrà essere ottenuto nel seguente modo:a_{1,1} =il prodotto della prima riga con la prima colonna.a_{1,1} =\begin{bmatrix}2&0&1\end{bmatrix}\cdot\begin{bmatrix}1\\5\\0\end{bmatrix} = \begin{bmatrix}2\cdot 1+0\cdot 5+1\cdot 0 = 2\end{bmatrix}Quindi svolgendo per tutti gli elementi il risultato finale sarà:\begin{bmatrix}2&0&1\\-1&-2&3\end{bmatrix}\cdot\begin{bmatrix}1&0&3&0\\5&-1&4&2\\0&1&-2&3\end{bmatrix} = \begin{bmatrix}2&1&43\\-11&5&-17&5\end{bmatrix}

Torna a matrici

Torna a definizioni matrici

Vai a determinante