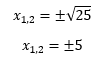Disequazioni di secondo grado intere – Esercizio 3
Disequazioni di secondo grado intere – Esercizio 3
Risolvi la seguente disequazione di secondo grado intera:
Per prima cosa in questa disequazione conviene cambiare il segno dei vari monomi in modo che il termine che precede x^2 sia positivo.
Questa disequazione è già ordinata pertanto possiamo iniziare a svolgere l’esercizio trovando l’equazione associata. Questo passaggio ci permetterà di trovare le radici dell’equazione e quindi i valori per le quali l’equazione stessa si annulla.
L’equazione ovviamente è di secondo grado e inoltre è pura perchè manca la variabile x e quindi il termine “b” della forma completa. Procediamo a risolvere:
Possiamo quindi dire che -5 e 5 sono le soluzioni dell’equazione associata. Troviamo adesso le soluzioni della disequazione. Per trovarle guardiamo il segno del termine “a” della disequazione (che è +1) e il verso della disequazione stessa (che è <). Poichè “a” è positivo e il segno della disequazione è minore diciamo che i segni sono discordi. Si considerano come intervalli di soluzione i valori interni alle radici come in figura:
e si scrive:
