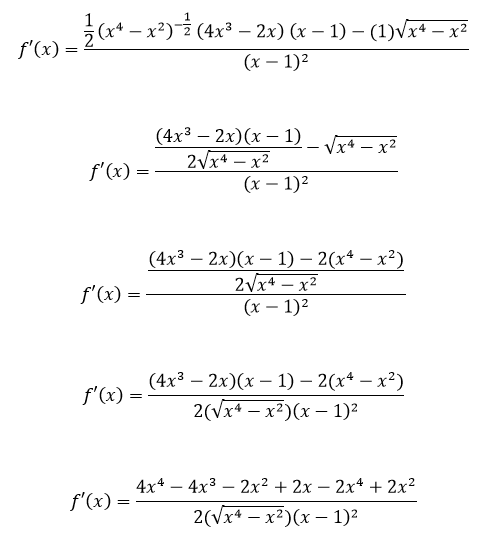Studio Funzione 1
Studiare la seguente funzione
Dominio
Per trovare il dominio della funzione la classifichiamo. Come possiamo vedere è una funzione fratta perchè la variabile x è al denominatore, e inoltre è irrazionale perchè è anche presente sotto una radice quadrata.
Per trovare il dominio quindi dobbiamo risolvere il seguente sistema di condizioni:
Derivata I
Studiamo ora la derivata prima. Per prima cosa, poichè dovremo applicare la regola di derivazione di una funzione fratta, ci conviene avere una sola funzione al numeratore e una al denominatore. Attualmente invece al numeratore è presente un prodotto di due funzioni. Portiamo quindi la funzione in un’altra forma:
A questo punto possiamo calcolare la derivata della funzione:
Eseguendo tutte le semplificazioni possiamo scrivere la derivata prima nel seguente modo:
A questo punto andiamo a studiare la derivata prima:
Per quanto riguarda il denominatore sappiamo che è sempre positivo perchè è un prodotto di quantità positive. Quindi sia il segno che i punti stazionari dipendono solo dal numeratore:
Scomponiamo per comodità con Ruffini il polinomio di terzo grado:
Grafico
Il grafico finale della funzione è :