Esercizio 3 – Intersezioni con gli assi

Trova le intersezioni con gli assi di una funzione razionale fratta:

Per risolvere il problema delle intersezioni con gli assi coordinati dobbiamo svolgere due sistemi:

Asse x

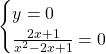
Dobbiamo quindi risolvere la seguente equazione fratta:

I valori che annulano questa frazioni sono quelli che annullano il numeratore posto il fatto che il denominatore invece non può mai essere nullo. Poniamo quindi come condizioni di esistenza:

pertanto 

Da notare che questo studio si affronta quando si calcola il dominio della funzione in quanto dobbiamo porre il denominatore diverso da zero.

Per trovare gli zeri della frazione risolviamo

Possiamo concludere che il sistema ha una coppia di soluzioni e quindi è presente un punto di intersezione con l’asse x:

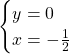
Asse y

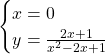
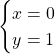
Il grafico mostra che quanto abbiamo studiato è corretto in quanto è presente un punto di intersezione con l’asse x e un punto di intersezione con l’asse y.

Torna a intesezioni con gli assi coordinati

Torna allo studio di funzioni

 

Comments

comments