Esercizio funzione esponenziale – Esercizio 5

21 Novembre 2019 gpalmieri Funzioni

Studiare la seguente funzione esponenziale (esercizio funzione esponenziale):

$f(x)=\frac{2e^x}{(x+1)^2}$

Dominio

Per prima cosa individuiamo il dominio della funzione cioè l’insieme dei valori che hanno una associazione con un valore nel codominio della funzione. Per trovare il dominio è necessario classificare la funzione. La funzione è razionale fratta e anche esponenziale. Per i fatto che è una funzione fratta, dobbiamo imporre che il denominatore della frazione sia diverso da zero:

$(x+1)^2 \neq 0$

$x+1 \neq 0$

$x \neq -1$

Il numeratore non pone problemi per il dominio in quanto è un esponenziale sommato ad un valore numerico. Concludiamo quindi che il dominio è il seguente intervallo di valori:

$D: (-\infty;-1) \cup (-1;+\infty)$

Intersezioni con gli assi

Il secondo problema da risolvere è quello di individuare le intersezioni della funzioni con gli assi coordinati. Per trovare le intersezioni è necessario risolvere due sistemi:

Asse x

$\begin{cases}y=0\\ \frac{2e^x}{(x+1)^2}=0 \end{cases}$

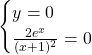
La frazione si annulla solo se il numeratore è nullo: $2e^x=0$ . L’esponenziale non può mai annullarsi quindi questa funzione non si interseca mai con l’asse delle x

Asse y

$\begin{cases}x=0\\y=\frac{2e^x}{(x+1)^2} \end{cases}$

$\begin{cases}x=0\\y=\frac{2e^0}{(0+1)^2} \end{cases}$

$\begin{cases}x=0\\y=\frac{2\ cdot (1)}{1} \end{cases}$

$\begin{cases}x=0\\y=2 \end{cases}$

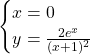
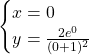
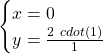
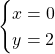
Esiste un punto di intersezione con l’asse y che ha le coordinate $P(0,2)$

Segno

Lo studio del segno ci permetterà di trovare l’insieme di positività (ovvero per quali valori del dominio la funzione è positiva) e quello di negatività. Per risolvere questo problema poniamo la funzione maggiore di zero:

$\frac{2e^x}{(x+1)^2}>0$

Poichè si tratta di una funzione fratta studiamo separatamente il segno del numeratore e del denominatore per poi effettuare il prodotto dei segni.

$N: 2e^x > 0 \forall x \in R$

$D: (x+1)^2 > 0 \forall x \in R$

La funzione è sempre positiva (al numeratore un esponenziale che è sempre strettamente positivo) e al denominatore un quadrato sempre positivo:

Limiti

Studiamo ora i limiti della funzione agli estremi del dominio:

1 Limite

$\lim_{x\to -\infty} \frac{2e^x}{(x+1)^2}$

$\frac{2e^{-\infty}}{(-\infty+1)^2}$

$e^{\frac{0}{+\infty}} = 0$

2 Limite

$\lim_{x\to 1^{-}} \frac{2e^x}{(x+1)^2}=$

$\frac{2e^{1}}{(1+1)^2}$

$e^{\frac{2}{0}} = +\infty$

3 Limite

$\lim_{x\to 1^{+}}\frac{2e^x}{(x+1)^2}=$

$\frac{2e^{1}}{(1+1)^2}$

$e^{\frac{2}{0}} = +\infty$

4 Limite

$\lim_{x\to +\infty}\frac{2e^x}{(x+1)^2}=$

$\frac{2e^{+\infty}}{(+\infty+1)^2}$

$\frac{\infty}{\infty}$

Questa è una forma indeterminata. Possiamo risolvere questa forma considerando il fatto che l’esponenziale tende ad infinito molto più velocemente rispetto alla potenza quindi il numeratore va ad infinito più velocemente rispetto al denominatore. Il risultato finale sarà quindi:

$\lim_{x\to +\infty} \frac{2e^x}{(x+1)^2}=+\infty$

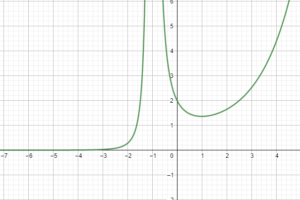
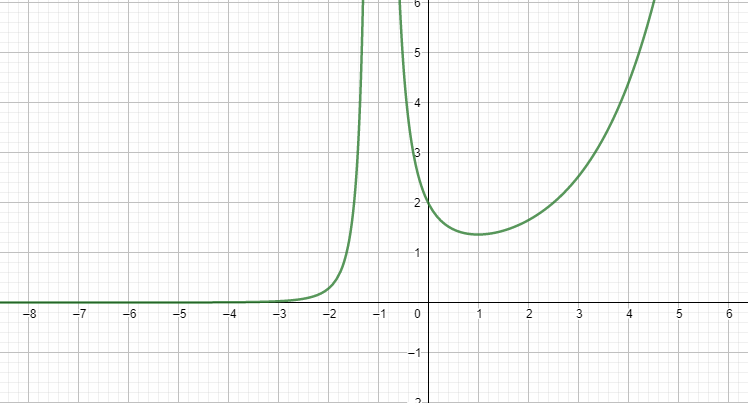
Dopo aver studiato i limiti possiamo tracciare il grafico qualitativo:

Asintoti

Dallo studio dei limiti troviamo un asintoto orizzontale in quanto:

$\lim_{x\to -\infty} \frac{2e^x}{(x+1)^2} =0$

Quindi la retta $y=0$ è asintoto orizzontale.

E’ presente anche un asintoto verticale in quanto:

$\lim_{x\to 1} \frac{2e^x}{(x+1)^2}=+\infty$

Quindi la retta $x=1$ è asintoto verticale.

Derivata 1

$f(x)=\frac{2e^x}{(x+1)^2}$

Per calcolare la derivata applichiamo la regola che si applica alle funzioni fratte:

$d[\frac{f(x)}{g(x)}] = \frac{f^{'}(x) g(x)-f(x)g^{'}(x)}{[g(x)]^2}$

$f^{'}(x)=\frac{(2e^x \cdot (x+1)^2) - (2e^x \cdot 2(x+1)^1 \cdot 1)}{(x+1)^4}$

$f^{'}(x)=\frac{2e^x \cdot (x+1)^2 - 2e^x \cdot 2(x+1)}{(x+1)^4}$

$f^{'}(x)=\frac{2e^x \cdot (x+1) \cdot (x+1-2)}{(x+1)^4}$

$f^{'}(x)=\frac{2e^x \cdot (x+1) \cdot (x-1)}{(x+1)^4}$

$f^{'}(x)=\frac{2e^x \cdot (x^2-1)}{(x+1)^4}$

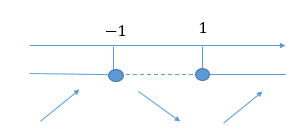
Studiamo ora il segno della derivata considerando tutti i fattori e facendo il prodotto dei segni. Il denominatore è sempre positivo quindi non influisce nel calcolo del segno.

$2e^x > 0 \forall x \in R$ (un esponenziale è sempre positivo)

$x^2-1 \geq 0$

$x^2-1=0$

$x^2 = 1$

$x = \pm \sqrt{1}$

$x<-1 o x>1$

Il punto -1 non appartiene al dominio della funzione (e della derivata prima) quindi non può essere considerato come punto stazionario. La funzione è crescente da $-\infty$ a $-1$ e da $1$ a $+/infty$ . La funzione decresce da -1 a 1 e per $x=1$ è presente un punto di minimo. Per trovare la coordinata y del minimo sostituiamo il valore 1 nella funzione:

$f(1)=\frac{2e^1}{(1+1)^2}$

$f(1)=\frac{2e}{4}$

$f(1)=\frac{e}{2}$

$M_{1}(1,\frac{e}{2})$

Derivata 2

$f^{'}(x)=\frac{2e^x \cdot (x^2-1)}{(x+1)^4}$

Per calcolare la derivata seconda applichiamo la regola del prodotto di due funzioni:

$f^{''}(x)=\frac{[2e^x(x^2-1)+2e^x(2x)] \cdot (x+1)^4 - 2e^x(x^2-1)\cdot4(x+1)^3\cdot 1}{(x+1)^8}$

$f^{''}(x)=\frac{2e^x(x^2-1+2x)(x+1)^4-2e^x \cdot 4(x+1)^4(x-1)}{(x+1)^8}$

$f^{''}(x)=\frac{2e^x (x+1)^4 (x^2-1+2x-4x+4)}{(x+1)^8}$

$f^{''}(x)=\frac{2e^x (x+1)^4 (x^2-2x+3)}{(x+1)^8}$

Come abbiamo fatto per la derivata prima studiamo il segno dei due fattori della derivata seconda e poi facciamo il prodotto dei segni separatamente. L’unico fattore che influenza il segno è (x^2-2x+3) perchè tutti gli altri sono positivi.

$x^2-2x+3 \geq 0$

$\Delta = (-2)^2 -12 = 4-12 = -8 <0$

La disequazione di secondo grado è sempre positiva e non si annulla mai quindi non sono presenti punti di flesso e la concavità della funzione è sempre rivolta verso l’alto come ci mostra il grafico (esercizio funzione esponenziale):

L	M	M	G	V	S	D
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30