Le funzioni esponenziali – Esercizio 6
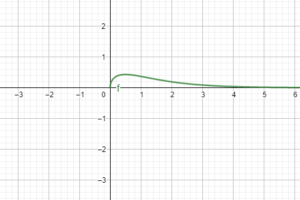
Studiare la seguente funzione esponenziale (esercizio funzione esponenziale):
![]()
Dominio
Per prima cosa individuiamo il dominio della funzione cioè l’insieme dei valori che hanno una associazione con un valore nel codominio della funzione. Per trovare il dominio è necessario classificare la funzione. La funzione è razionale fratta, esponenziale ed irrazionale. Per i fatto che è una funzione fratta, dobbiamo imporre che il denominatore della frazione sia diverso da zero e per la sua irrazionalità dobbiamo imporre il contenuto della radice quadrata maggiore o uguale a zero:
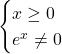
La seconda equazione è sempre soddisfatta perchè un esponenziale non si annulla mai. Per questo motivo sappiamo che il dominio della funzione è “deciso” dalla prima disequazione:
Concludiamo quindi che il dominio è il seguente intervallo di valori:
![]()
Intersezioni con gli assi
Il secondo problema da risolvere è quello di individuare le intersezioni della funzioni con gli assi coordinati. Per trovare le intersezioni è necessario risolvere due sistemi:
Asse x
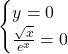
La frazione si annulla solo se il numeratore è nullo: ![]() .
.
![]()
La radice è nulla solo se il contenuto è nullo:
![]()
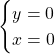
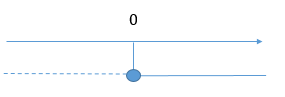
Esiste quindi un punto di intersezione ![]() .
.
Asse y
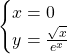
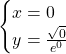
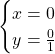
Il punto che individuiamo è sempre lo stesso ![]()
La funzione quindi si interseca con l’origine degli assi.
Segno
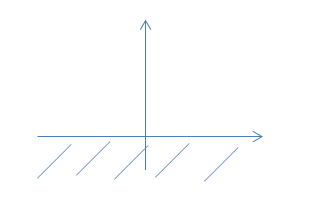
Lo studio del segno ci permetterà di trovare l’insieme di positività (ovvero per quali valori del dominio la funzione è positiva) e quello di negatività. Per risolvere questo problema poniamo la funzione maggiore di zero:
![]()
Poichè si tratta di una funzione fratta studiamo separatamente il segno del numeratore e del denominatore per poi effettuare il prodotto dei segni.
![]()
![]()
La funzione è sempre positiva (al numeratore un esponenziale che è sempre strettamente positivo) e al denominatore un quadrato sempre positivo:
Limiti
Studiamo ora i limiti della funzione agli estremi del dominio:
1 Limite
![]()
![]()
Il risultato è una forma indeterminata del tipo ![]() . Possiamo risolvere questa forma ricordando che un esponenziale va ad infinito molto più velocemente rispetto ad una potenza. Per questo motivo il numeratore va ad infinito in maniera molto più veloce rispetto al numeratore e risulta che il risultato del limite sia zero.
. Possiamo risolvere questa forma ricordando che un esponenziale va ad infinito molto più velocemente rispetto ad una potenza. Per questo motivo il numeratore va ad infinito in maniera molto più veloce rispetto al numeratore e risulta che il risultato del limite sia zero.
![]()
Non ci sono altri limiti da studiare.
Asintoti
Dallo studio dei limiti troviamo un asintoto orizzontale in quanto:
![]()
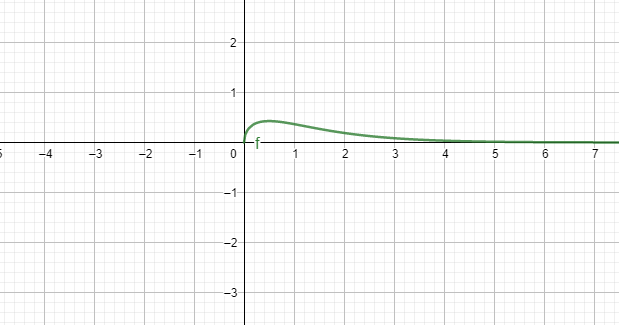
Quindi la retta ![]() è asintoto orizzontale.
è asintoto orizzontale.
Derivata 1
![]()
Per calcolare la derivata applichiamo la regola che si applica alle funzioni fratte:
![]()
Per comodità nella risoluzione riscriviamo la frazione nel seguente modo:
![]()
![]()
![]()
![]()
![]()
![]()
Studiamo ora il segno della derivata considerando tutti i fattori e facendo il prodotto dei segni. Il denominatore è sempre positivo quindi non influisce nel calcolo del segno. Studiamo il numeratore:
![]()
Primo fattore
![]()
Secondo fattore
![]()
![]()
![]()
![]()
In sintesi:
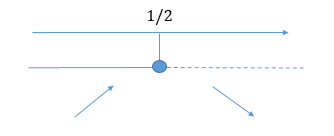
Per ![]() la derivata prima si annulla quindi è l’ascissa di un punto stazionario. Poichè la funzione cresce si annulla in
la derivata prima si annulla quindi è l’ascissa di un punto stazionario. Poichè la funzione cresce si annulla in ![]() e poi decresce si tratta di un punto di massimo. Possiamo trovare l’ordinata del punto sostituendo il valore nella funzione:
e poi decresce si tratta di un punto di massimo. Possiamo trovare l’ordinata del punto sostituendo il valore nella funzione:
![]()
Derivata 2
![]()
![]()
…
Torna a studio di funzioni esponenziali
Torna a matematica