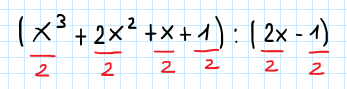Metodo di Ruffini esercizio

31 Gennaio 2021 gpalmieri Divisione polinomi

Metodo di Ruffini esercizio. Risolvi la seguente divisione utilizzando il metodo di Ruffini:

$(x^3+2x^2+x+1):(2x-1)$

In questo caso il binomio divisore non si trova nella forma corretta $x-a$ con $a$ numero reale qualsiasi. Questo a causa della presenza del coefficiente $2$ davanti al termine $x$ . Per “toglierlo” possiamo dividere primo e secondo membro per $2$ :

Semplificando il polinomio riscritto sarà:

$(\frac{1}{2}x^3+x^2+\frac{1}{2}x+\frac{1}{2}):(x-\frac{1}{2})$

Abbassiamo il primo termine e moltiplichiamo per il $\frac{1}{2}$ :

Procediamo moltiplicando il secondo termine:

$\frac{1}{2}+\frac{5}{8}=\frac{4+5}{8}=\frac{9}{8}$

$\frac{1}{2}+\frac{9}{16}=\frac{8+9}{16}=\frac{17}{16}$

Quoziente: $\frac{1}{2}x^2+\frac{5}{4}x+\frac{9}{8}$

Resto: $\frac{17}{16}$

Clicca qui per la teoria.

Torna a divisione polinomi esercizi

Comments

comments

Lascia un commento divisione polinomi, metodo ruffini, ruffini

Lascia un commento Annulla risposta